Wstępna wiedza wymagana dla lepszego zrozumienia problematyki artykułu dostępna tutaj:
- 5-cio częściowy cykl artykułów Jarosława Dolińskiego z Elektroniki Praktycznej p.t. "CRC doda Ci pewności" część 1,
- Artykuł na angielskiej Wiki,
- Publikacja "Hashing Algorithms", rozdział "The 32 bit CRC Algorithm" [link].
- Opracowanie Ross N. Williamsa [link]
- Opracowanie Ross N. Williamsa [link]
Dalsze analizy będą opierały się na podstawach teoretycznych z powyższych źródeł.
Na wstępie wyjaśnienie akronimu CRC - Cyclic Redundancy Code. Czasem stosowane jest rozwinięcie Cyclic Redundancy Check, jednak nie do końca ono pasuje Dobrze wytłumaczone jest to tutaj. Na angielskiej Wikipedii stosowany jest ten drugi termin. Wygląda na to, że zależne to jest w dużej mierze od kontekstu :)
Na celownik naszych analiz weźmiemy szeroko stosowany algorytm CRC-32, choć rozważania można uogólnić na wszystkie typy wielomianów generujących.
Na celownik naszych analiz weźmiemy szeroko stosowany algorytm CRC-32, choć rozważania można uogólnić na wszystkie typy wielomianów generujących.
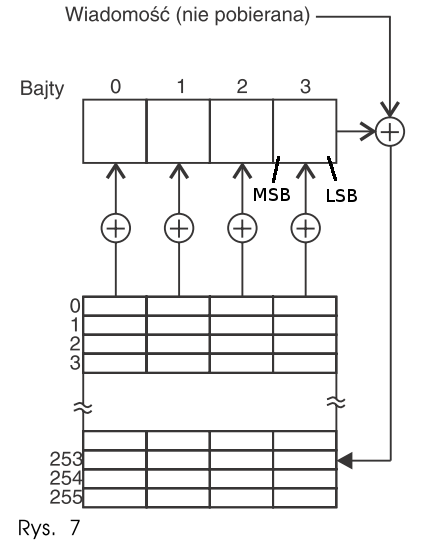
CRC-32 wykorzystywane jest m.in. w Ethernecie. Dane przesyłane w ramce Ethernetowej wysyłane są w specyficznej kolejności: Bajty w formacie Big endian, natomiast poszczególne bity są przesyłane w formacie Little endian - najpierw najmniej znaczący bit LSB (najmłodszy) [źródło]. Z tego powodu do generowania kodu CRC wykorzystuje się odwrócony algorytm tablicowy, który przedstawiono graficznie na poniższym rysunku:
żródło: Artykuł: "CRC doda Ci pewności, cz.3"
Co istotne, bity pobierane są właśnie w kolejności najpierw LSB, a następnie MSB, co zaznaczono na rysunku. Dyskusyjne może być jedynie numerowanie bajtów - choć to kwestia czysto umowna. Należy tylko pamiętać o obowiązującym formacie Big endian.
Tablica dla CRC-32 przedstawiona jest poniżej. Postaram się wyjaśnić w jaki sposób liczone są jej składowe.
uint32_t crc32_table[256] = 0, 0x77073096, 0xEE0E612C, 0x990951BA, 0x076DC419, 0x706AF48F, 0xE963A535, 0x9E6495A3, 0x0EDB8832, 0x79DCB8A4, 0xE0D5E91E, 0x97D2D988, 0x09B64C2B, 0x7EB17CBD, 0xE7B82D07, 0x90BF1D91, 0x1DB71064, 0x6AB020F2, 0xF3B97148, 0x84BE41DE, 0x1ADAD47D, 0x6DDDE4EB, 0xF4D4B551, 0x83D385C7, 0x136C9856, 0x646BA8C0, 0xFD62F97A, 0x8A65C9EC, 0x14015C4F, 0x63066CD9, 0xFA0F3D63, 0x8D080DF5, 0x3B6E20C8, 0x4C69105E, 0xD56041E4, 0xA2677172, 0x3C03E4D1, 0x4B04D447, 0xD20D85FD, 0xA50AB56B, 0x35B5A8FA, 0x42B2986C, 0xDBBBC9D6, 0xACBCF940, 0x32D86CE3, 0x45DF5C75, 0xDCD60DCF, 0xABD13D59, 0x26D930AC, 0x51DE003A, 0xC8D75180, 0xBFD06116, 0x21B4F4B5, 0x56B3C423, 0xCFBA9599, 0xB8BDA50F, 0x2802B89E, 0x5F058808, 0xC60CD9B2, 0xB10BE924, 0x2F6F7C87, 0x58684C11, 0xC1611DAB, 0xB6662D3D, 0x76DC4190, 0x01DB7106, 0x98D220BC, 0xEFD5102A, 0x71B18589, 0x06B6B51F, 0x9FBFE4A5, 0xE8B8D433, 0x7807C9A2, 0x0F00F934, 0x9609A88E, 0xE10E9818, 0x7F6A0DBB, 0x086D3D2D, 0x91646C97, 0xE6635C01, 0x6B6B51F4, 0x1C6C6162, 0x856530D8, 0xF262004E, 0x6C0695ED, 0x1B01A57B, 0x8208F4C1, 0xF50FC457, 0x65B0D9C6, 0x12B7E950, 0x8BBEB8EA, 0xFCB9887C, 0x62DD1DDF, 0x15DA2D49, 0x8CD37CF3, 0xFBD44C65, 0x4DB26158, 0x3AB551CE, 0xA3BC0074, 0xD4BB30E2, 0x4ADFA541, 0x3DD895D7, 0xA4D1C46D, 0xD3D6F4FB, 0x4369E96A, 0x346ED9FC, 0xAD678846, 0xDA60B8D0, 0x44042D73, 0x33031DE5, 0xAA0A4C5F, 0xDD0D7CC9, 0x5005713C, 0x270241AA, 0xBE0B1010, 0xC90C2086, 0x5768B525, 0x206F85B3, 0xB966D409, 0xCE61E49F, 0x5EDEF90E, 0x29D9C998, 0xB0D09822, 0xC7D7A8B4, 0x59B33D17, 0x2EB40D81, 0xB7BD5C3B, 0xC0BA6CAD, 0xEDB88320, 0x9ABFB3B6, 0x03B6E20C, 0x74B1D29A, 0xEAD54739, 0x9DD277AF, 0x04DB2615, 0x73DC1683, 0xE3630B12, 0x94643B84, 0x0D6D6A3E, 0x7A6A5AA8, 0xE40ECF0B, 0x9309FF9D, 0x0A00AE27, 0x7D079EB1, 0xF00F9344, 0x8708A3D2, 0x1E01F268, 0x6906C2FE, 0xF762575D, 0x806567CB, 0x196C3671, 0x6E6B06E7, 0xFED41B76, 0x89D32BE0, 0x10DA7A5A, 0x67DD4ACC, 0xF9B9DF6F, 0x8EBEEFF9, 0x17B7BE43, 0x60B08ED5, 0xD6D6A3E8, 0xA1D1937E, 0x38D8C2C4, 0x4FDFF252, 0xD1BB67F1, 0xA6BC5767, 0x3FB506DD, 0x48B2364B, 0xD80D2BDA, 0xAF0A1B4C, 0x36034AF6, 0x41047A60, 0xDF60EFC3, 0xA867DF55, 0x316E8EEF, 0x4669BE79, 0xCB61B38C, 0xBC66831A, 0x256FD2A0, 0x5268E236, 0xCC0C7795, 0xBB0B4703, 0x220216B9, 0x5505262F, 0xC5BA3BBE, 0xB2BD0B28, 0x2BB45A92, 0x5CB36A04, 0xC2D7FFA7, 0xB5D0CF31, 0x2CD99E8B, 0x5BDEAE1D, 0x9B64C2B0, 0xEC63F226, 0x756AA39C, 0x026D930A, 0x9C0906A9, 0xEB0E363F, 0x72076785, 0x05005713, 0x95BF4A82, 0xE2B87A14, 0x7BB12BAE, 0x0CB61B38, 0x92D28E9B, 0xE5D5BE0D, 0x7CDCEFB7, 0x0BDBDF21, 0x86D3D2D4, 0xF1D4E242, 0x68DDB3F8, 0x1FDA836E, 0x81BE16CD, 0xF6B9265B, 0x6FB077E1, 0x18B74777, 0x88085AE6, 0xFF0F6A70, 0x66063BCA, 0x11010B5C, 0x8F659EFF, 0xF862AE69, 0x616BFFD3, 0x166CCF45, 0xA00AE278, 0xD70DD2EE, 0x4E048354, 0x3903B3C2, 0xA7672661, 0xD06016F7, 0x4969474D, 0x3E6E77DB, 0xAED16A4A, 0xD9D65ADC, 0x40DF0B66, 0x37D83BF0, 0xA9BCAE53, 0xDEBB9EC5, 0x47B2CF7F, 0x30B5FFE9, 0xBDBDF21C, 0xCABAC28A, 0x53B39330, 0x24B4A3A6, 0xBAD03605, 0xCDD70693, 0x54DE5729, 0x23D967BF, 0xB3667A2E, 0xC4614AB8, 0x5D681B02, 0x2A6F2B94, 0xB40BBE37, 0xC30C8EA1, 0x5A05DF1B, 0x2D02EF8D };
Generator (wielomian generujący) dla CRC-32:
0x04C11DB7
postać odwrócona generatora CRC-32:
0xEDB88320
odwrócenie polega na lustrzanym odbiciu wszystkich bitów.
Zauważmy na analogię odwracania bitów podczas zmiany kolejności z takiej: najpierw MSB potem LSB na taką: najpierw LSB potem MSB. Ta druga wykorzystywana jest właśnie w Ethernecie. W zależności od kolejności przetwarzania nadchodzących bitów stosuje się właśnie zwykły bądź odwrócony algorytm tablicowy.
Generator standardowy i odwórcony, są ze sobą bardzo powiązane, jednak istnieje między nimi bardzo subtelna różnica, Wykorzystując jako generator podstawowy wartość generatora odwróconego otrzymamy zupełnie inny wynik sumy kontrolnej CRC - to dosyć logiczne, zmieniamy dzielnik, zatem reszta z dzielenia jest inna. Jednak wartość generatora odwróconego wykorzystywana jest w obliczeniach tablic dla odwróconego algorytmu tablicowego. Dzięki jego wykorzystaniu nie musimy odwracać obliczonej wartości przed wstawieniem jej do tablicy. Zamiast generatora 0x04C11DB7 wykorzystujemy jego odwróconą wartość 0xEDB88320 otrzymując finalnie obliczony rejestr, którego nie musimy już odwracać - unikamy tym samym tej żmudnej operacji "lustrzanego odbijania bitów".
Wykorzystanie wartości generatora odwróconego (ale nie samego generatora!) utrudnia zrozumienie mechanizmu tworzenia wartości tablic dla odwróconego algorytmu tablicowego.
W powyższych zdaniach słowo wartość zostało celowo wyróżnione, aby podkreślić, iż mówimy tylko o wartości 0xEDB88320 jako lustrzanym odbiciu (odwróceniu) generatora, jednak nie należy go mylić z faktycznym generatorem jakim jest 0x04C11DB7.
Dalsze przykłady powinny wyjaśnić o co chodzi.
Kod źródłowy programu do obliczania elementów tablicy CRC32:
uint32_t crc32_table[256];
static void make_crc32_table(void){
uint32_t c, i, k;
for (i = 0; i < 256; i++){
c = i;
for (k = 0; k < 8; k++) {
if (c & 1) c = 0xEDB88320 ^ (c >> 1);
else c >>= 1;
}
crc32_table[i] = c;
}
}
Program tworzy tablicę dla generatora o wartości 0x04C11DB7 jednak wartość rejestru c jest XORowana z odwróconą wartością generatora czyli 0xEDB88320 (ale nie generatorem odwróconym!)
Dla bajtu równego 0 składnik tablicy crc32_table[0]=0. W bajcie nie ma żadnych bitów=1, dlatego nie wykonujemy ani jednego XORowania.
Dla bajtu równego 128 (zapis bitowy MSB 1000 0000 LSB) składnik tablicy crc32_table[128]=0xEDB88320. Poniższy rysunek przedstawia schemat tworzenia tegoż składnika:
Dodatkowo na rysunku znajdują się strzałki wskazujące który bit za co odpowiada, wraz z opisem kolejności kroków (na kolejnych są pomijane). Gdy dany bit jest równy 1 uzupełniamy rejestr wartością odwróconego generatora czyli 0xEDB88320 (zaznaczony kolorem czerwonym). Dokonując XORowania wszystkich bitów otrzymujemy zatem ten sam wynik. Przykład został wybrany celowo na początek, ponieważ należy do najprostszych.
Jeszcze jeden podobny i prosty przykład na rozgrzewkę:
Dla bajtu równego 16 (zapis bitowy MSB 0001 0000 LSB) składnik tablicy crc32_table[16]=0x1DB71064. Schemat tworzenia na rysunku:
Zdawać by się mogło że nic nas już nie może zaskoczyć ;) Dla bajtu równego 1 obliczenia powinny być już tylko formalnością. Sprawdźmy zatem.
Dla bajtu równego 1 (zapis bitowy MSB 0000 0001 LSB) składnik tablicy crc32_table[1]=0x77073096. Spróbujmy użyć naszego schematu:
Zamiast spodziewanego 0x77073096 otrzymujemy 0x01DB7106. Gdzie zatem ten diabeł tkwiący zawsze w szczegółach? :) Nie można zapominać, iź podczas przesuwania rejestru wcześniejsze wartości bitów równych 1 także są brane pod uwagę. Jeśli wychodzącym bitem jest 1, należy przesunąć rejestr i dokonać kolejnego XORowania z wartością odwróconego generatora (porównaj algorytm z literatury na początku wpisu). Zaznaczono to na poniższym rysunku kolorem zielonym:
Należy przyjrzeć się temu bardzo uważnie. Pomimo zerowego bitu w bajcie na tej pozycji i tak dokonujemy XORowania. Bity poszukiwanego bajtu (w powyższym przypadku MSB 0000 0001 LSB) są od samego początku nieustannie XORowane z wartością odwróconego generatora.
Zgodnie z powyższym będzie dochodziło do sytuacji dodatkowego XORowania pomimo zerowej wartości odpowiedniego bitu w bajcie lub braku tego XORowania w sytuacji odwrotnej (czyli gdy bit wskazywałby taką konieczność). Cała sytuacja jest spowodowana wartością dobranego generatora (konkretniej wykorzystywanej wartości odwortnej generatora), ponieważ 6 bit jest równy 1 - właśnie tutaj znajduje się nasz diabeł powodujący zamieszanie ;)
Brak XORowania widoczny jest w przykładzie na obliczenie bajtu=255.
Dla bajtu równego 255 (zapis bitowy MSB 1111 1111 LSB) składnik tablicy crc32_table[255]=0x2D02EF8D. Schemat tworzenia na rysunku (zielonym kolorem wyróżniono fragmenty w których nie XORuje się rejestru):
Znając już dobrze mechanizn tworzenia poszczególnych składników tablicy dla odwróconego algorytmu tablicowego, możemy przejść do zademonstrowania dlaczego właściwie wykorzystuje się wartość odwróconego generatora do ich obliczania. Wykorzystamy w tym celu obliczanie bajtu o wartości 145.
Najpierw z wykorzystaniem wartości odwróconego generatora tj. 0xEDB88320. Czyli tak samo jak wszystkie wcześniejsze przykłady.
Dla bajtu równego 145 (zapis bitowy MSB 1111 1111 LSB) składnik tablicy crc32_table[145]=0x8708A3D2. Schemat tworzenia:
Obliczenie z wykorzystaniem podstawowej wartości generatora 0x04C11DB7 przedstawia się następująco:
Zmieniono kierunek przesuwania rejestru oraz kolejność bitów w poszukiwanym bajcie 145 (zapis bitowy LSB 1000 1001 MSB - choć to tylko kwestia zapisu mająca na celu ukazanie kolejności wysuwania poszczególnych bitów z rejestru). Najważniejszą różnicą w stosunku do poprzedniej metody jest fakt, iź musimy odwrócić wynik XORowania przed uzyskaniem wyniku końcowego. Tym samym widoczne jest teraz, dlaczego wcześniej stosowaliśmy wartość odwróconego generatora zamiast podstawowej. Dzięki temu końcowe odwracanie nie jest konieczne. Otrzymaliśmy ten sam wynik przez odwrócenie generatora przed XORowaniem.
Dlaczego ważne jest odpowiednie dobranie generatora (tym samym wartości odwróconej do niego)? Urządzenia w sieci Ethernet oraz np. 1-Wire wysyłają bity w kolejności "najpierw LSB", suma kontrolna CRC obliczana jest sprzętowo w locie bit po bicie z wykorzystaniem danego generatora. W związku z tym jeśli użylibyśmy generatora odwróconego uzyskalibyśmy zupełnie inną sumę CRC.
Na szczęście wiele nowoczesnych układów elektronicznych (w tym mikrokontrolerów) posiada specjalizowane peryferia umożliwiające obliczanie sumy kontrolnej CRC w locie, dlatego nie jest wtedy konieczne wykorzystywanie metod programowych m.in. tablicowej.
Jako dodatek mały przykład, iż wszystkie tutejsze rozważania można z powodzeniem zastosować do innych generatorów np. CRC-8 Dallas/Maxim. Poniżej przykład obliczenia drugiej wartości z tablicy - dla bajtu 1 (tablice dostępne są w internecie):
W tej chwili mały trick :) Odpowiednie ustawienie wartości rozpisanego na bity poszukiwanego bajtu (żółte pola na powyższym rysunku) pozwala na dosyć wygodne sprawdzanie czy następny wiersz ma być uzupełniony zerami, czy też wartością odwróconego generatora. Po prawej stronie XORujemy kolejne kolumny przesuwając się w lewo i dodając pod spodem kolejne wiersze. W przypadku jeśli wynik XORowania wynosi 1 uzupełniamy kolejny wiersz wartością odwróconego generatora, w przeciwnym razie wstawiamy same zera. Opanowanie tej metody pozwoli na błyskawiczne obliczenie CRC nawet ręcznie. Zachęcam do przejrzenia we wszystkich wcześniejszych przykładach.
Tylko bez przesady z tymi "ręcznymi" obliczeniami - od czego mamy komputery :)
Za poświęcony czas dziękuję i do następnego wpisu!
Michał